
MÉCANIQUE DU VOL
GTR VOL EN MONTÉE
- Influence de Wu
- Influence du poids mg
- Influence de l'altitude
- Influence du vent
Equation du vol en montée
Nous avons:
- `Ø` assiette est l'angle formé entre l'axe du fuselage et l'horizontale ;
- `γ` la pente est l'angle formé entre l'horizontale et l'axe des vitesses ;
- `α` l'incidence est l'angle formé entre l'axe longitudinal de l'avion et la direction du vent relatif (axe des vitesses).

Rappelons que nous ferons les hypothèses suivantes:
- le vol est symétrique.
- le centre de poussée et le centre de gravité sont confondus.
- le vecteur vitesse est constant.
- l'angle de calage de la voilure est ` 0 ` (`α` avion = `α` profil).
- L'incidence `α` est négligeable devant la pente
` γ` d'où `Ø` = ` γ`
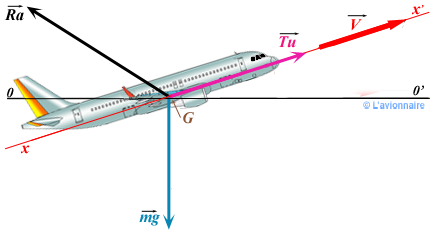
Comme en vol horizontal, trois grandes forces s'exercent sur un aéronef en montée:
- Le poids `\vec{mg}`
- La traction `\vec{Tu}`
- La résultante aérodynamique `\vec{Ra}`
Le mouvement étant rectiligne uniforme : `\vec{Ra}+\vec{Tu}+\vec{mg}= \vec{0}`
Ces trois grandes forces se décomposent suivant deux axes:
- L'axe de sustentation z z' toujours perpendiculaire au vecteur vitesse.
- L'axe de propulsion x x' toujours parallèle au vecteur vitesse.
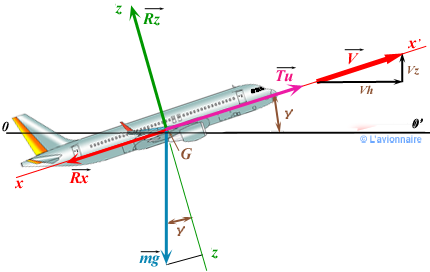
Nous avons:
Équation de sustentation : `Rz = mg cos γ`
Équation de propulsion: `Tu = Rx +mg sin γ`
La traction est égale à ` Rx` comme en palier plus un supplément `ΔTu` pour compenser la composante du poids `mg sin γ` .
Vitesse verticale Vz
En multipliant par `V ` nous pouvons transformer l'équation de puissance en:
- `Tu .V ` représente la puissance nécessaire pour la montée
- `Rx .V` représente la puissance nécessaire au vol horizontal à la vitesse `Vv` .
- ` mg . V sin γ` est le supplément de puissance qu'il faut ajouter au vol horizontal si l'on veut monter à la même vitesse.
Ce qui donne :
`ΔW` étant l'excédant de puissance.
La vitesse de vol `V` peut se décomposer en une vitesse horizontale et une vitesse verticale `Vz`

Pente de montée
Or les `Vz` ont une valeur faible par rapport à la vitesse propre, on peut donc considérer que :
Puisque en vol horizontal nous avons : `Wn = Rx .V ` et ` mg = Rz`
Une pente de 5 % est égale à une pente de 0,05 radian .
Et le calcul simplifié est :
Attention : Pour que la formule soit correcte, il faut utiliser pour les Vz les pieds ft (feet) par minutes et pour les vitesses les noeuds Kt (Knot).
Vol en montée à Vz maximale
Nous supposerons que `Tu` est constante quelle que soit `V`, Voir GTR Courbes Tu/Tn donc `Wu = Tu V` sera une droite passant par l'origine.
Si l'avion vole entre `V1` et `V2` , il dispose d'un excédent de puissance ` ΔWu` et le vol en montée sera alors possible. `ΔWu` sera maximal au point où une parallèle à `Wu` tangente la courbe `Wn`.
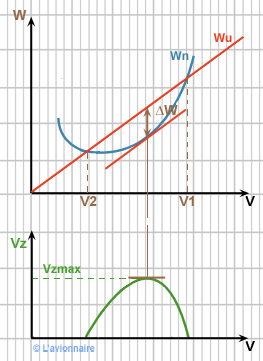
Ci-dessus nous voyons que la `Vz` maximale sera atteinte à l'incidence du point ` ΔWu` maxi.
Sur `GTR` les meilleures performances de montée sont obtenues à des incidences relativement faibles, donc à des vitesses élevées.
Vol en montée à Pente maximale
La pente maxi sera indiquée par la droite `Wu` passant par l'origine et tangentant la courbe `Wn`.
Pour `Tu` donnée `γ=\frac{Tu}{mg}` étant constant `\frac{1}{ƒ}` est mini
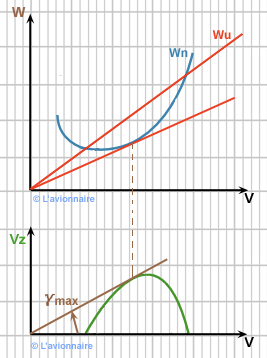
LA PENTE SERA MAXIMALE A L'INCIDENCE DE FINESSE MAXIMALE
influence de Wu ( ou Tu) sur le vol en montée
Nous avons vu que `Vz=\frac{Wu-Wn}{mg}`
A `mg`, `\text{incidence}` et `ρ` constants, la puissance nécessaire `Wn` est constante.
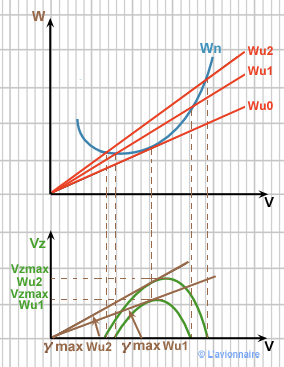
Si `Tu` augmente à incidence donnée :
- La `Vz max` augmente
- L'incidence de la `Vz max` diminue
- `γmax` (pente) augmente
- L'incidence de `γ max` reste constante
Influence du poids mg sur le vol en montée
Pendant le vol la consommation de carburant va provoquer une diminution de `m_1g` à `m_2g` (poids).
`mg` influe sur la courbe `Wn` et influe également sur `Vz` car `Vz =\frac{Wu-Wn}{mg}`
Et influe sur la pente : `γ=\frac{Tu}{mg} -\frac{1}{ƒ}`
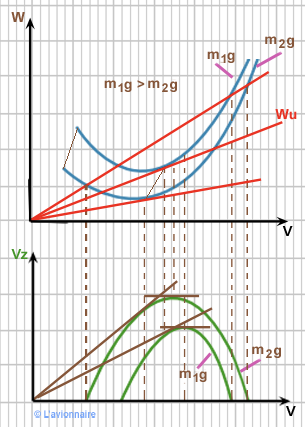
Si `i` (incidence), `ƒ` et `V` sont fixés :
LORSQUE `mg` DIMINUE A INCIDENCE CONSTANTE `Vz` ET `γ` AUGMENTENT.
Les vitesses de `Vz max` et de `γmax` diminuent.
Influence de l'altitude sur le vol en montée
Si l'altitude augmente la poussée `Tu` diminue et donc `Wu` diminue aussi. Et `Wn` augmente à incidence donnée.
`Vz =\frac{Wu-Wn}{mg}` et `γ=\frac{Tu}{mg} -\frac{1}{ƒ}` diminuent avec l'altitude.
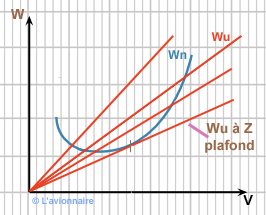
L'INCIDENCE DE FINESSE MAXIMALE SERA L'INCIDENCE DU PLAFOND DE PROPULSION
Influence des volets sur le vol en montée
Pendant la phase de décollage, un braquage de volets faible va diminuer la vitesse de décollage et par conséquent la distance de décollage. Par contre la pente maximale de montée se fait à l'incidence de finesse maximale, or tous braquages de volets diminue la finesse maximale.
La sortie des volets diminue la pente de montée.
Influence du vent sur le vol en montée
Le vent horizontal n'a aucune influence sur la `Vz` .
Vent de face
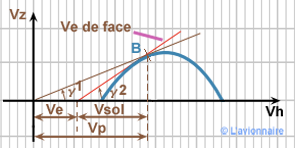
Si l'avion monte à l'incidence du point `B`, sa pente sera `γ1`. Mais pour un observateur au sol, l'avion monte sous l'angle de `γ2`. La pente sol est plus grande que la pente air et si la vitesse du vent était suffisamment grande, l'avion donnerait alors l'impression de monter à la verticale.
Vent arrière
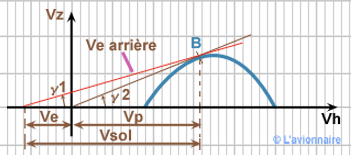
Même raisonnement mais cette fois la pente air est plus grande que la pente sol.

